Eigenfaces

Example for Principal Component Analysis (PCA) on face images also known as Eigenfaces

Theory

If you are new on PCA, first see PCA_2D_example.

Results

The code given below produces the following output.

Some examples of the face images of the olivetti face dataset.

The first 100 principal components extracted from the dataset. The components focus on characteristics like glasses, lighting direction, nose shape, …

The cumulative sum of the Eigenvalues show how ‘compressable’ the dataset is.

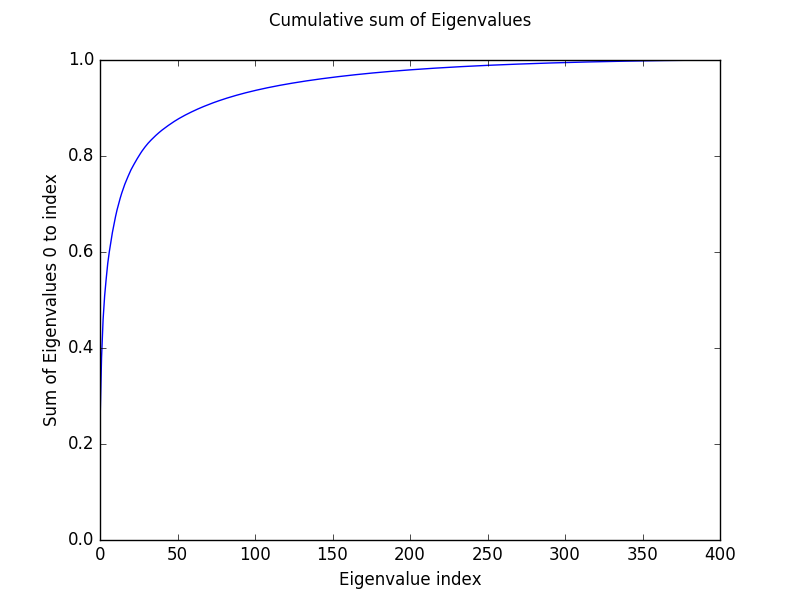
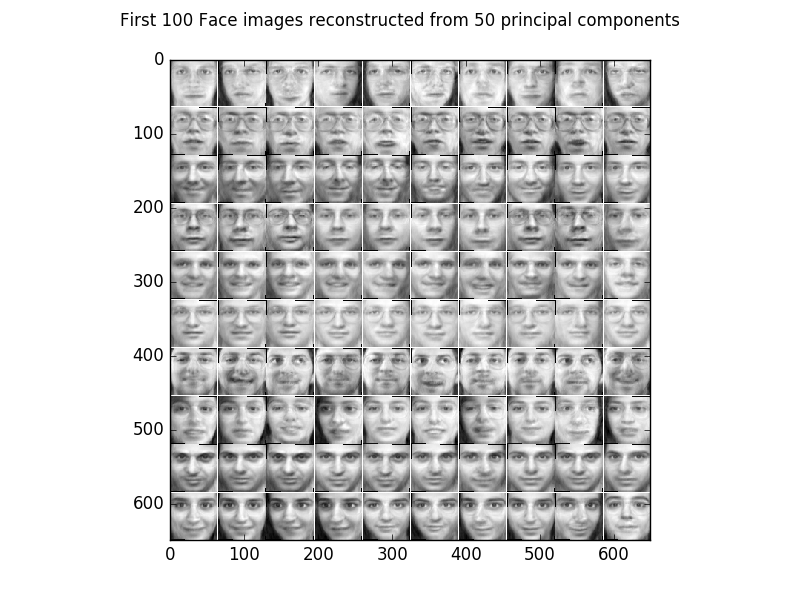
For example using only the first 50 eigenvectors retains 87,5 % of the variance of data and the reconstructed images look as follows.

For 200 eigenvectors we retain 98,0 % of the variance of the data and the reconstructed images look as follows.

Comparing the results with the original images shows that the data can be compressed to 50 dimensions with an acceptable error.

Source code

""" Example for Principal component analysis on face images (Eigenfaces).

    :Version:
        1.1.0

    :Date:
        22.04.2017

    :Author:
        Jan Melchior

    :Contact:
        JanMelchior@gmx.de

    :License:

        Copyright (C) 2017 Jan Melchior

        This file is part of the Python library PyDeep.

        PyDeep is free software: you can redistribute it and/or modify
        it under the terms of the GNU General Public License as published by
        the Free Software Foundation, either version 3 of the License, or
        (at your option) any later version.

        This program is distributed in the hope that it will be useful,
        but WITHOUT ANY WARRANTY; without even the implied warranty of
        MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
        GNU General Public License for more details.

        You should have received a copy of the GNU General Public License
        along with this program.  If not, see <http://www.gnu.org/licenses/>.

"""

# Import numpy, PCA, input output module, and visualization module
import numpy as numx
from pydeep.preprocessing import PCA
import pydeep.misc.io as io
import pydeep.misc.visualization as vis

# Set the random seed
# (optional, if stochastic processes are involved we get the same results)
numx.random.seed(42)

# Load data (download is not existing)
data = io.load_olivetti_faces(path='olivettifaces.mat')

# Specify image width and height for displaying
width = height = 64

# PCA
pca = PCA(input_dim=width * height)
pca.train(data=data)

# Show the first 100 eigenvectors of the covariance matrix
eigenvectors = vis.tile_matrix_rows(matrix=pca.projection_matrix,
                                    tile_width=width,
                                    tile_height=height,
                                    num_tiles_x=10,
                                    num_tiles_y=10,
                                    border_size=1,
                                    normalized=True)
vis.imshow_matrix(matrix=eigenvectors,
                  windowtitle='First 100 Eigenvectors of the covariance matrix')

# Show the first 100 images
images = vis.tile_matrix_rows(matrix=data[0:100].T,
                              tile_width=width,
                              tile_height=height,
                              num_tiles_x=10,
                              num_tiles_y=10,
                              border_size=1,
                              normalized=True)
vis.imshow_matrix(matrix=images,
                  windowtitle='First 100 Face images')

# Plot the cumulative sum of teh Eigenvalues.
eigenvalue_sum = numx.cumsum(pca.eigen_values / numx.sum(pca.eigen_values))
vis.imshow_plot(matrix=eigenvalue_sum,
                windowtitle="Cumulative sum of Eigenvalues")
vis.xlabel("Eigenvalue index")
vis.ylabel("Sum of Eigenvalues 0 to index")
vis.ylim(0, 1)
vis.xlim(0, 400)

# Show the first 100 Face images reconstructed from 50 principal components
recon = pca.unproject(pca.project(data[0:100], num_components=50)).T
images = vis.tile_matrix_rows(matrix=recon,
                              tile_width=width,
                              tile_height=height,
                              num_tiles_x=10,
                              num_tiles_y=10,
                              border_size=1,
                              normalized=True)
vis.imshow_matrix(matrix=images,
                  windowtitle='First 100 Face images reconstructed from 50 '
                              'principal components')

# Show the first 100 Face images reconstructed from 120 principal components
recon = pca.unproject(pca.project(data[0:100], num_components=200)).T
images = vis.tile_matrix_rows(matrix=recon,
                              tile_width=width,
                              tile_height=height,
                              num_tiles_x=10,
                              num_tiles_y=10,
                              border_size=1,
                              normalized=True)
vis.imshow_matrix(matrix=images,
                  windowtitle='First 100 Face images reconstructed from 200 '
                              'principal components')

# Show all windows.
vis.show()