Big binary RBM on MNIST¶
Example for training a centered and normal binary restricted Boltzmann machine on the MNIST handwritten digit dataset. The model has 500 hidden units, is trained for 200 epochs (That takes a while, reduce it if you like), and the log-likelihood is evaluated using annealed importance sampling.
It allows to reproduce the results from the publication How to Center Deep Boltzmann Machines. Melchior et al. JMLR 2016.. Running the code as it is for example reproduces a single trial of the plot in Figure 9. (PCD-1) for $dd^b_s$.
Theory¶
If you are new on RBMs, first see RBM_MNIST_small.
For an analysis of the advantage of centering in RBMs see How to Center Deep Boltzmann Machines. Melchior et al. JMLR 2016.
Results¶
The code given below produces the following output.
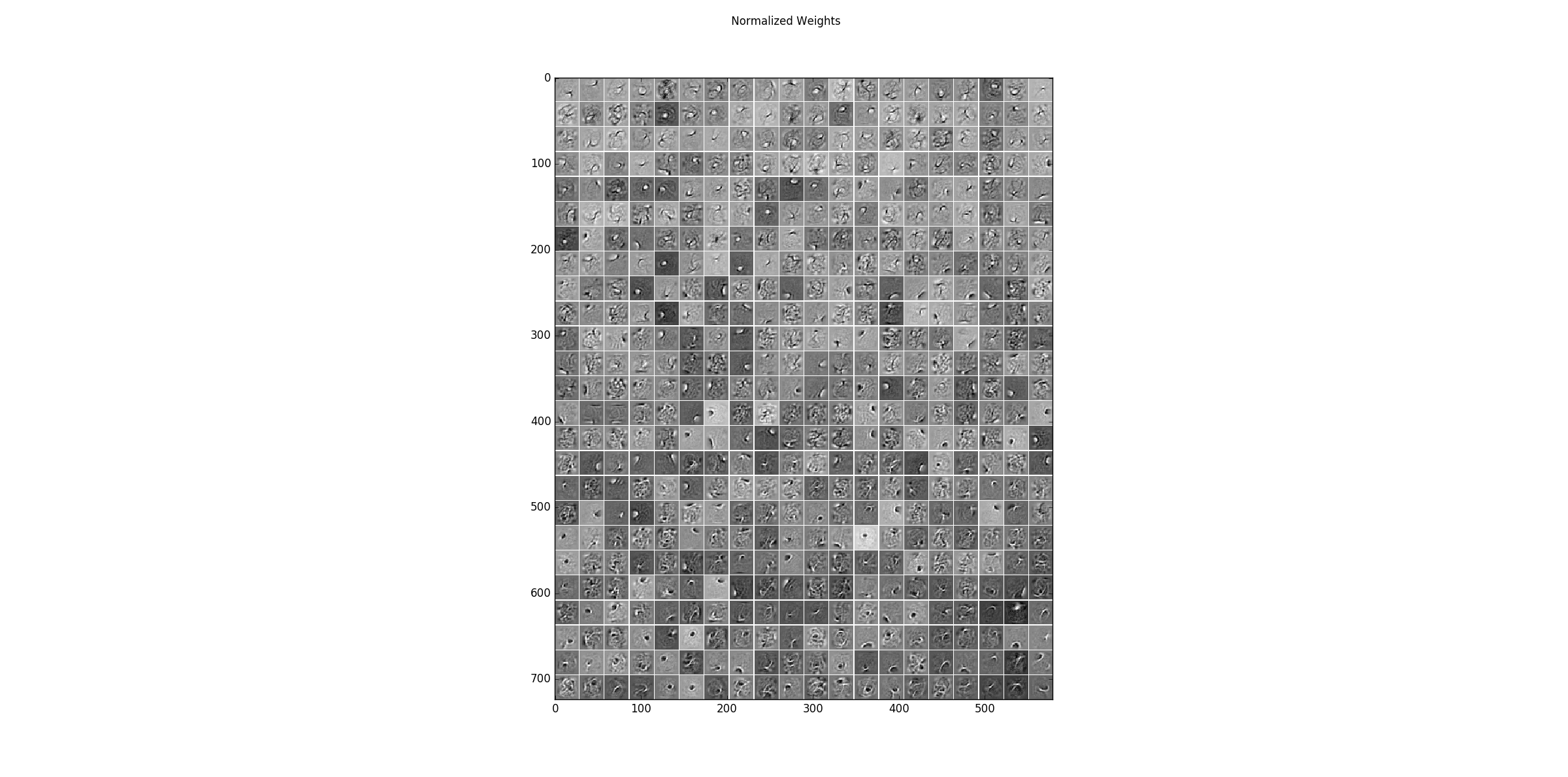
Learned filters of a centered binary RBM with 500 hidden units on the MNIST dataset. The filters have been normalized such that the structure is more prominent.
Sampling results for some examples. The first row shows some training data and the following rows are the results after one Gibbs-sampling step starting from the previous row.
The log-Likelihood is estimated using annealed importance sampling (optimistic) and reverse annealed importance sampling (pessimistic).
Training time: 1:18:12.536887
AIS Partition: 968.971299741 (LL train: -82.5839850187, LL test: -84.8560508601)
reverse AIS Partition: 980.722421486 (LL train: -94.3351067638, LL test: -96.6071726052)
Now we have a look at the filters learned for a normal binary RBM with 500 hidden units on the MNIST dataset. The filters have also been normalized such that the structure is more prominent.
Sampling results for some examples. The first row shows the training data and the following rows are the results after one Gibbs-sampling step starting from the previous row.
Training time: 1:16:37.808645
AIS Partition: 959.098055647 (LL train: -128.009777345, LL test: -130.808849443)
reverse AIS Partition: 958.714291654 (LL train: -127.626013352, LL test: -130.42508545)
The structure of the filters and the samples are quite similar. But the samples for the centered RBM look a bit sharper and the log-likelihood is significantly higher. Note that you can reach better values with normal RBMs but this highly depends on the training setup, whereas centering is rather robust to that.
For real valued input see also GRBM_natural_images.
Source code¶
""" Example using a big BB-RBMs on the MNIST handwritten digit database.
:Version:
1.1.0
:Date:
24.04.2017
:Author:
Jan Melchior
:Contact:
JanMelchior@gmx.de
:License:
Copyright (C) 2017 Jan Melchior
This file is part of the Python library PyDeep.
PyDeep is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program. If not, see <http://www.gnu.org/licenses/>.
"""
import numpy as numx
import pydeep.rbm.model as model
import pydeep.rbm.trainer as trainer
import pydeep.rbm.estimator as estimator
import pydeep.misc.io as io
import pydeep.misc.visualization as vis
import pydeep.misc.measuring as mea
# normal/centered RBM --> 0.0/0.01
update_offsets = 0.0
# Set random seed (optional)
numx.random.seed(42)
# Input and hidden dimensionality
v1 = v2 = 28
h1 = 25
h2 = 20
# Load data (download is not existing)
train_data, _, valid_data, _, test_data, _ = io.load_mnist("mnist.pkl.gz", True)
train_data = numx.vstack((train_data, valid_data))
# Training paramters
batch_size = 100
epochs = 200
# Create centered or normal model
if update_offsets <= 0.0:
rbm = model.BinaryBinaryRBM(number_visibles=v1 * v2,
number_hiddens=h1 * h2,
data=None,
initial_weights=0.01,
initial_visible_bias=0.0,
initial_hidden_bias=0.0,
initial_visible_offsets=0.0,
initial_hidden_offsets=0.0)
else:
rbm = model.BinaryBinaryRBM(number_visibles=v1 * v2,
number_hiddens=h1 * h2,
data=train_data,
initial_weights=0.01,
initial_visible_bias='AUTO',
initial_hidden_bias='AUTO',
initial_visible_offsets='AUTO',
initial_hidden_offsets='AUTO')
trainer_pcd = trainer.PCD(rbm, num_chains=batch_size)
# Measuring time
measurer = mea.Stopwatch()
# Train model
print('Training')
print('Epoch\t\tRecon. Error\tLog likelihood \tExpected End-Time')
for epoch in range(1, epochs + 1):
# Loop over all batches
for b in range(0, train_data.shape[0], batch_size):
batch = train_data[b:b + batch_size, :]
trainer_pcd.train(data=batch,
epsilon=0.01,
update_visible_offsets=update_offsets,
update_hidden_offsets=update_offsets)
# Calculate reconstruction error and expected end time every 10th epoch
if epoch % 10 == 0:
RE = numx.mean(estimator.reconstruction_error(rbm, train_data))
print('{}\t\t{:.4f}\t\t\t{}'.format(
epoch, RE, measurer.get_expected_end_time(epoch, epochs)))
else:
print(epoch)
# Stop time measurement
measurer.end()
# Print end time
print("End-time: \t{}".format(measurer.get_end_time()))
print("Training time:\t{}".format(measurer.get_interval()))
# Approximate partition function by AIS (tends to overestimate)
logZ_approx_AIS = estimator.annealed_importance_sampling(rbm)[0]
print("AIS Partition: {} (LL train: {}, LL test: {})".format(logZ_approx_AIS,
numx.mean(estimator.log_likelihood_v(rbm, logZ_approx_AIS, train_data)),
numx.mean(estimator.log_likelihood_v(rbm, logZ_approx_AIS, test_data))))
# Approximate partition function by reverse AIS (tends to underestimate)
logZ_approx_rAIS = estimator.reverse_annealed_importance_sampling(rbm)[0]
print("reverse AIS Partition: {} (LL train: {}, LL test: {})".format(
logZ_approx_rAIS,
numx.mean(estimator.log_likelihood_v(rbm, logZ_approx_rAIS, train_data)),
numx.mean(estimator.log_likelihood_v(rbm, logZ_approx_rAIS, test_data))))
# Reorder RBM features by average activity decreasingly
reordered_rbm = vis.reorder_filter_by_hidden_activation(rbm, train_data)
# Display RBM parameters
vis.imshow_standard_rbm_parameters(reordered_rbm, v1, v2, h1, h2)
# Sample some steps and show results
samples = vis.generate_samples(rbm, train_data[0:30], 30, 1, v1, v2, False, None)
vis.imshow_matrix(samples, 'Samples')
# Display results
vis.show()